Mit Funktionen kann man noch mehr machen!
Grundwissen PDF
Grundbegriffe
Stelligkeit
nullstellige, einstellige, zweistellige, dreistellige Funktionen
Bereichsoperator
Datenflussdiagramm
Termnotation (infix und praefix)
Zusammenhänge
Buch Informatik 2, Klettverlag, S. 38 – 39
Das Wichtigste in Kürze:
Die Anzahl der Eingabewerte (Parameter) einer Funktion bestimmt ihre Stelligkeit.
Beispiele:
Textfunktionen Mathematische Funktionen Datums-und Zeitfunktionennullstellig PI()
ZUFALLSZAHL() HEUTE()
JETZT()
einstellig LÄNGE(Text)
GLÄTTEN(Text) ABS(Zahl)
VORZEICHEN(Zahl) JAHR(Zeitangabe)
zweistellig IDENTISCH(Text1;Text2) RUNDEN(Zahl;Nachkommastellen)
REST(Zah1; Zahl2) TAGE(Datum2;Datum1)
dreistellig TEIL(Text;Anfang;Anzahl)
SUCHEN(Suchtext;Text;Position) ZEIT(Stunde;Minute;Sekunde)
Einige Funktionen haben eine nichtfestgelegte Stelligkeit, d.h.man kann ihnen unterschiedlich viele Parameter mitgeben.
Dazu gehören die häufig verwendeten mathematischen Funktonen SUMME(), MITTELWERT(), MAX(), MIN(),ANZAHL() und ANZAHL2().
Beispiel: ····SUMME(A1;A2;B4;B5;C3), aber auch SUMME(A1;A2;B4)
Bei Funktionen mit nichtfestgelegter Stelligkeit kann man als Parameter auch einen Bereichsoperatoreinsetzen.
Beispiel:SUMME(A3:A10
) berechnet die Summe aller Zahlen in der Spalte von
A3 bis A10
SUMME(A3:H3)) berechnet die Summe aller Zahlen in der Zeile von A3 bis H3
SUMME(A3:H10) berechnet die Summe aller Zahlen im Rechteck zwischen A3 bis H10
Funktionen lassen sich unterschiedlich darstellen.
Für uns wichtig ist das Datenflussdiagramm und die Termnotation.
Datenflussdigramme werden besonders bei schwierigeren Aufgaben (verkettete Funktionen, siehe später!) eine Hilfe sein.
Die Termnotation wird als Formel in das Rechenblatt eingegeben.
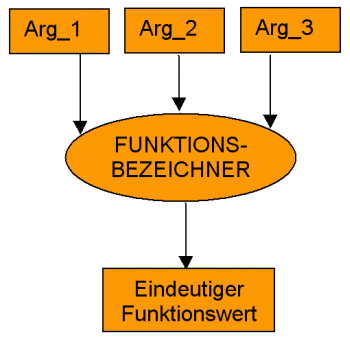
Termnotation
(in Präfix-Schreibweise)
FUNKTIONSBEZEICHNER(Arg_1; Arg_2; Arg_3)
Die Termnotation der meisten Funktionen erfolgt in Präfix-Schreibweise.
Das bedeutet, dass der Funktionsbezeichner am Anfang steht und dahinter in einer Klammer der oder die Parameter.
Beispiel: SUMME(A4;A5)
Für einige zweistellige Funktionen gibt es auch (aus Gewohnheitsgründen) die Infix-Schreibweise.
Der Funktionsbezeichner steht zwischen beiden Parametern und ist meist nur eine kurzes Operatorsymbol.
Beispiel: A4 + A5
Aufgaben PDF
Beginne zunächst mi dem folgenden Arbeitsblatt:
Arbeitsblatt zu Datenflüssen
Summenfunktion
Dieses Rechenblatt berechnet die Summe der ersten 100 natürlichen Zahlen.
Nur die Zahl 1 wird als Startzahl vorgegeben, alle anderen Zellen sind berechnet!
Für die Zeilensumme und die Spaltensumme verwendest du den Bereichsoperator :
Beispiel: In Zelle B13 steht die Formel =Summe(B3:B12)
Der Bereichsopertor kann nicht nur auf einzelne Spalten oder Zeilen angewendet werden, sondern auch auf rechteckige Zellbereiche.
Beispiel: In Zelle A17 steht die Formel =Summe(B3:K12)
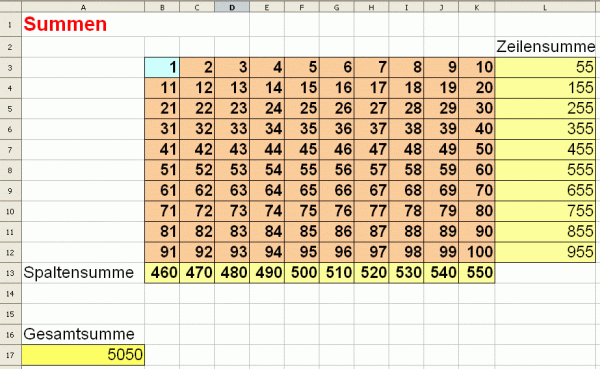
Ändere nun die Startzahl 1 ab , z. B. auf 0.
Versuche auch eine negative Startzahl! Welche negative Startzahl liefert als Gesamtsumme 0?
Dateiname: summe100
Präfix- und Infixschreibweise
Vom Mathematikunterricht ist man gewohnt, für die Grundrechenarten die Infix-Schreibweise zu verwenden.
Beispiel: Man schreibt 15 + 6,3 oder 15 * 6,3
In Tabellenkalkulationsprogrammen gibt es auch die Präfix-Notation
Beispiel: Man schreibt SUMME(15;6,3) oder PRODUKT(15;6,3)
Allerdings muss man ein paar Feinheiten beachten.
Erstelle dazu dieses Rechenblatt. In den Zellen B6 bis B10 wurde die Infix-Schreibweise verwendet, in den Spalten C6 bis C10 die Präfix-Schreibweise.
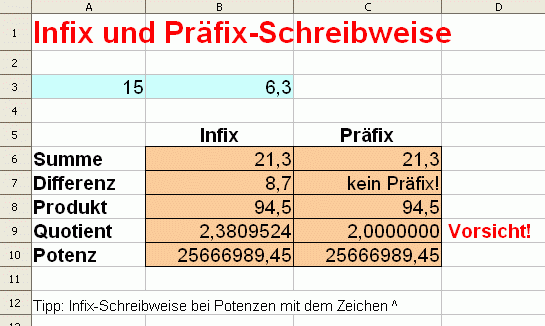
Beachte vor allem die unterschiedliche Bedeutung von 15/6,3 und QUOTIENT(15;6,3).
Die Präfix-Notation QUOTIENT(15;6,3) gibt den ganzzahigen Anteil bei der Division.
Dateiname: infix_praefix
Schaltjahre (vereinfacht)
Alle Zellen außer A4 sind berechnet!
Verwende für die Formel in Spalte C eine geeignete mathematische Funktion.
Die Zellen in Spalte D sind nur anders formatierte Kopien der Zellen aus Spalte C.
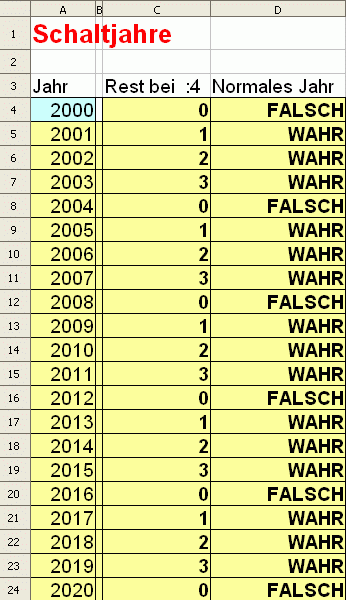
Beachte, dass die Tabelle für andere Zeiträume falsche Ergebnisse liefern kann. Näheres dazu später!
Dateiname: schaltjahr_1
Tabelle von Potenzen
Erstelle ein Rechenblatt dieser Art.
Die rot und gelb unterlegten Felder sind berechnet.
So steht in Zelle C5 die Funktion POTENZ($B5;C$4) in Präfixschreibweise.
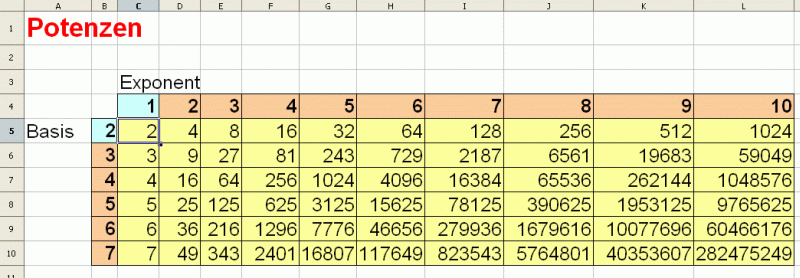
Kennst du auch die Infix-Schreibweise der Potenzfunktion? Teste sie!
ISBN
Jedes Buch hat eine ISBN, die Internationale Standardbuchnummer.
Sie ist 13-stellig. Aus ihr kann man das Land, den Verlag und die Verlagsnummer erschließen.
Die dreizehnte Ziffer der ISBN ist die Prüfziffer.
Die wird wie folgt berechnet:
Die ersten 12 Ziffern werden abwechselnd mit 1 und 3 multipliziert, wobei man bei der ersten Zifferlinks mit dem Faktor 1 beginnt.
Dann addiert man die Produktwerte.
Der Rest bei Division durch 10 wird von 10 subtrahiert und ergibt die Prüfziffer.
Bei Rest 0 ist die Prüfziffer 0. (Diesen Sonderfall kannst du zunächst vernachlässigen)
Erstelle ein Rechenblatt, das die Prüfziffer nach diesem Schema berechnet.
Teste dein Berechnungsschema an der ISBN des Informatikbuchs: 978-3-12-731668-1 oder an anderen ISBN.
Dateiname:· isbn_1
